- Vamos a revisar en esta oportunidad cómo se procede en la toma de decisiones frente a una situación médica determinada, empleando los conocimientos que adquirimos a lo largo del desarrollo de esta sección, y especialmente lo explicado en las últimas entregas sobre análisis económico.
- En dicho análisis suelen emplearse diferentes recursos o modelos, que permiten llegar a una decisión razonada que toma en cuenta datos médicos objetivos, la mejor evidencia de estudios observacionales o aleatorizados, pero también situaciones particulares, el perfil de la población considerada, las preferencias de los pacientes, e, idealmente, datos económicos locales.
- Entre los modelos empleados destacan el Árbol de Decisiones, el Modelo de Markov y la Simulación de Montecarlo
Árbol de decisiones
- Es una representación gráfica, frente a un problema de salud que debe resolverse, de las diversas opciones que se presentan, con las diferentes evoluciones, probabilidad de cada una y valoración económica de cada una, en términos de costo efectividad, costo utilidad o costo beneficio, y que permite entonces adoptar la mejor decisión.
- Un elemento esencial de los árboles de decisión son los nodos (momentos en los cuales se abre más de una posibilidad, de decisión inicialmente y de los diversos resultados probables esperables tras cada decisión).
- Cada vez que debe tomarse una decisión la situación se grafica con un cuadrado (nodo de decisión). Frente a cada decisión que se toma se plantean diferentes evoluciones. No sabemos a priori cuál será la evolución que ocurra, tenemos incertidumbre al respecto. Esos momentos en que se abren diferentes posibilidades se grafican con círculos (nodos de chance o incertidumbre). Los resultados definitivos de haber tomado una decisión y de haber ocurrido una evolución determinada se grafican con triángulos (nodos terminales).
- Los nodos correspondientes a una decisión se unen entre sí con segmentos de recta, y constituyen las ramas del árbol. Cada evento y la probabilidad del mismo se anotan en la rama correspondiente a ese evento. Es muy importante definir claramente el orden temporal de los eventos. El resultado final se anota junto al nodo terminal.
- El resultado final varía según el análisis considerado. Como ya vimos, en un estudio costo efectividad los resultados se miden en años de vida ganados, o la obtención de alguna modificación en un parámetro vital, o eventos evitados, las llamadas unidades de efectividad. En un estudio costo utilidad los resultados se miden en utilidades, unidades de efectividad ajustados por calidad, por ejemplo, AVAC. En un análisis costo beneficio los resultados se miden en unidades monetarias.
- A modo de ejemplo, vamos a considerar una patología determinada, para la cual hay dos tratamientos posibles: las drogas A y B. Cada una de estas drogas puede ser exitosa o fracasar. Por otra parte, podemos instituir el tratamiento basándonos solamente en el diagnóstico clínico (signos, síntomas) o realizar un estudio complementario en busca de una determinada condición, que puede a su vez estar presente (test positivo) o ausente (test negativo).
- En la Figura 1 está representado frente a la presencia de la patología un primer nodo de decisión (cuadrado amarillo 1) entre no hacer o hacer el estudio complementario. Si el estudio complementario se lleva a cabo, aparece un nodo de chance (círculo rojo 1) respecto de si el resultado será positivo o negativo.
- Los cuadrados amarillos 2 a 4 representan los nodos de decisión que habrá que tomar sobre usar la droga A o B si no se hizo el estudio, o si se hizo con resultado positivo o negativo. Y los círculos rojos 2 a 7, los nodos de chance de éxito o fracaso con la droga A o B en cada uno de los casos.
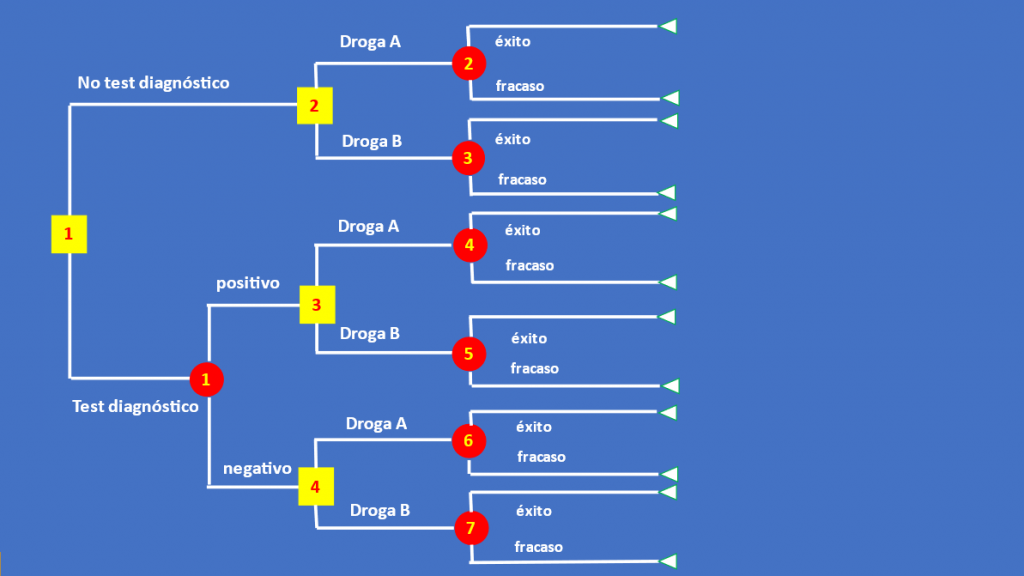
- Consideremos ahora las diferentes probabilidades en los diversos nodos de chance. (Figura 2). Las ramas que se desprenden del círculo 1 explicitan la probabilidad de resultado positivo (40%) o negativo (60%) frente al test diagnóstico. Las ramas que se desprenden de los círculos 2 a 7 muestran la chance de éxito o fracaso con el uso de la droga A (círculos 2, 4 y 6) o B (círculos 3, 5 y 7).
- Debe notarse que las probabilidades citadas no son arbitrarias. Por ejemplo, la probabilidad de éxito de la droga A en ausencia del test diagnóstico (72%, círculo 2) surge de la combinación de probabilidades de éxito de la misma droga si el test se llevara a cabo: si el test es positivo (40% de las veces) un 60% de éxito (círculo 4) y si es negativo (el 60% de las oportunidades) un 80% de éxito (círculo 6). Un 60% de éxito el 40% de las veces y un 80% de éxito el 60% restante se traducen en forma global en un éxito del 72%: (0.6 x 0.4) + (0.8 x 0.6) = 0.24 + 0.48= 0.72. Las mismas consideraciones valen para la probabilidad de fracaso de A, y para las probabilidades de éxito o fracaso de B
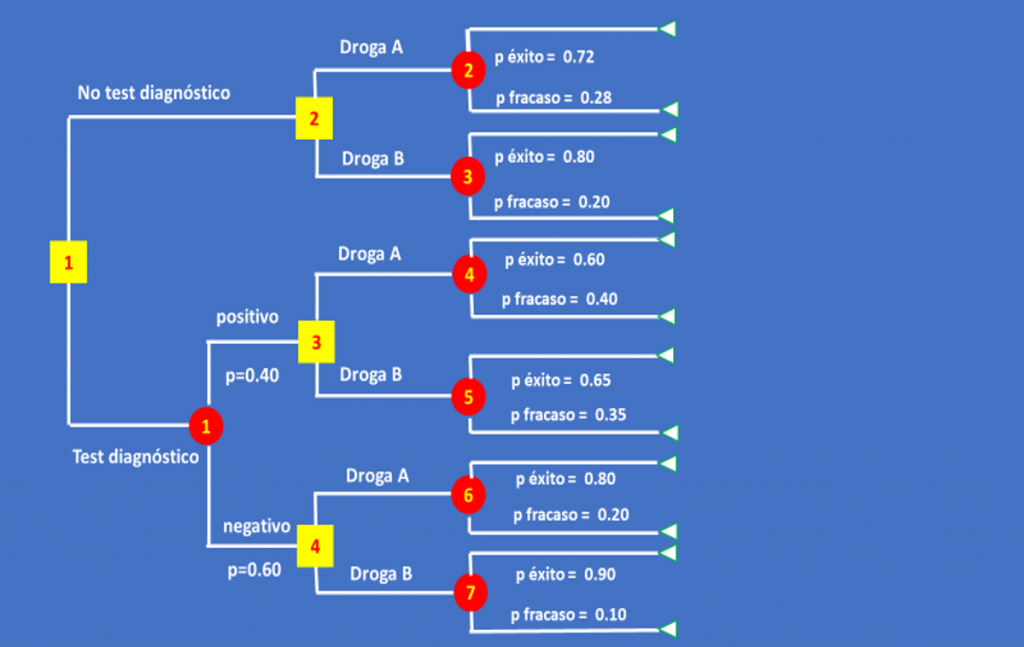
- Como dijimos, los triángulos al final de cada rama del árbol (nodos terminales) señalan la evolución esperada tras cada decisión, de acuerdo con el efecto de la droga y la probabilidad de éxito o fracaso en cada situación. Supongamos que la expectativa de vida (el resultado que exploramos inicialmente) es de 5 años si el tratamiento A es exitoso, 4 años si es exitoso el tratamiento B, y solo 1 año si cualquiera de ambos fracasa (Figura 3)
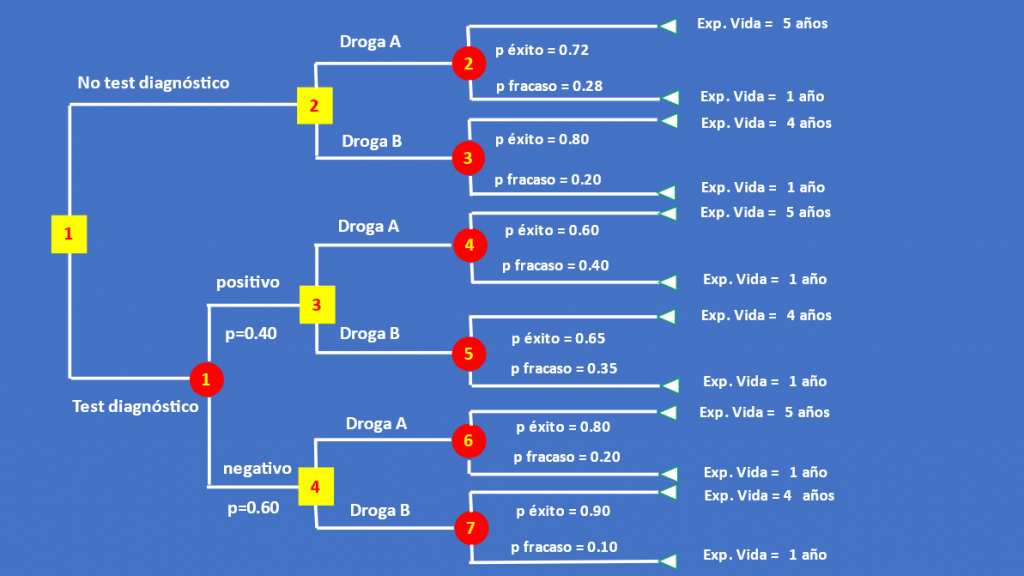
- Es claro que en realidad el resultado final de cada rama debe tener en cuenta en forma integrada la expectativa de vida que cada droga ofrece, pero también la probabilidad de éxito o fracaso en cada rama del árbol, de manera que, avanzando sobre el particular, en cada nodo terminal mostramos ahora el producto de la expectativa de vida por la probabilidad implicada en cada caso (Figura 4)
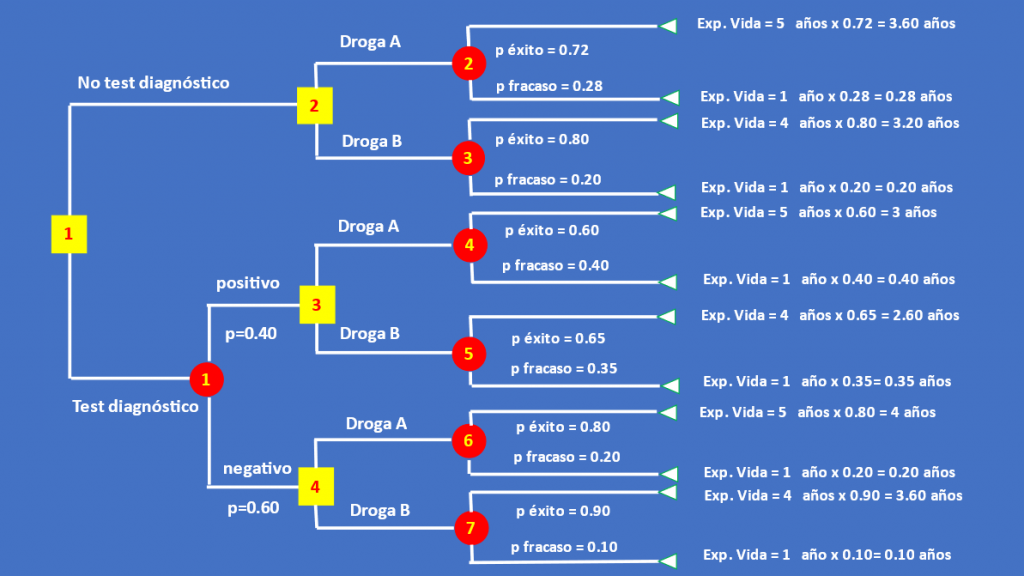
- Como vemos, entonces, cada nodo terminal se asocia finalmente a un determinado resultado o valor esperado.
- Por ejemplo, 3,6 años es la expectativa de vida si se decide no realizar el test diagnóstico (nodo de decisión o cuadrado 1), se decide emplear la droga A (nodo de decisión o cuadrado 2) y el tratamiento es exitoso (rama superior del nodo de chance o círculo 2).
- Y, en cambio, solo 0,1 años es la expectativa de vida si, habiendo realizado el test diagnóstico (nodo de decisión o cuadrado 1) y siendo el mismo negativo (nodo de chance o círculo 1), se opta por usar la droga B (nodo de decisión o cuadrado 4) y el tratamiento fracasa (rama inferior del nodo de chance o círculo 7)
- ¡Llegamos a la mitad del camino! En la próxima entrega veremos cómo continúa la interpretación del Árbol de Decisiones
Lecturas sugeridas
- Chapter 6. Expected value decision making. En Sox H, Higgins M, Owens D. Medical Decision Making. 2nd ed. Wiley-Blackwell 2013
- Gupta N et al. Cost-Effectiveness Analysis and Decision Modelling: A Tutorial for Clinicians. J Clin Exp Hepatol 2020;10(2):177-184






